Navegar por el vasto océano de la Inteligencia Artificial (IA) implica descubrir cómo las máquinas adquieren conocimiento y razonan. Uno de los faros guía en esta travesía es la lógica de predicados, una herramienta crucial que permite representar y manipular estructuras de conocimiento con precisión y eficiencia.
La lógica de predicados, una piedra angular en el edificio de la IA. Con su ayuda, las máquinas pueden llegar a razonar de forma precisa, tomando decisiones fundamentadas en los datos y reglas que se les han impartido.
La lógica de predicados, también referida como cálculo de predicados o lógica de primer orden, es un avance respecto a la lógica proposicional, ofreciendo un manejo más refinado y sofisticado de la información. Al permitirnos hacer afirmaciones sobre "todos" o "algunos" elementos de un conjunto a través de cuantificadores y variables, esta forma de lógica nos proporciona una mayor flexibilidad y profundidad en nuestras declaraciones lógicas.
Marco teórico
La lógica de predicados o lógica de primer orden es un sistema formal utilizado en lógica matemática e informática para expresar declaraciones y razonar sobre las relaciones entre objetos de manera precisa y rigurosa.
En la lógica de predicados, se utilizan variables, constantes, predicados, cuantificadores y conectivas lógicas para construir oraciones llamadas fórmulas. Estos son los componentes clave:
· Variables: Símbolos que representan objetos o entidades no especificados. Por ejemplo, x, y, z son variables.
· Constantes: Símbolos que representan objetos o entidades específicas. Por ejemplo, "Juan" o "5" pueden ser constantes.
· Predicados: Expresiones que describen propiedades o relaciones entre objetos. Los predicados pueden tener uno o más argumentos y devuelven un valor de verdad (verdadero o falso) en función de los valores de esos argumentos. Por ejemplo, "Mayor(x, y)" representa el predicado de que x es mayor que y.
· Cuantificador universal (∀): Representa "para todo" o "para cada". Por ejemplo, ∀x (P(x)) significa "P se cumple para todo x".
· Cuantificador existencial (∃): Representa "existe" o "hay al menos uno". Por ejemplo, ∃x (P(x)) significa "Existe un x para el cual P se cumple".
· Conectivas lógicas: Conectivas como negación (~), conjunción (Y, ∧), disyunción (O, ∨), implicación (→) y equivalencia (↔) se utilizan para combinar y manipular fórmulas.
Utilizando estos componentes, podemos construir declaraciones lógicas complejas y razonar sobre ellas de manera sistemática. La lógica de predicados proporciona una base para demostraciones matemáticas, razonamiento formal, demostración automatizada de teoremas y modelado de diversos aspectos del conocimiento y los cálculos.
Ejemplo
Podemos plantear un ejemplo basado en la familia de la siguiente forma:
1. Existe al menos una madre en la familia, ∃x Madre(x, y).
Esta fórmula dice que hay al menos una persona x que es madre de alguna persona y en la familia.
2. Todos los hijos tienen un padre. ∀x Hijo(x, y) → ∃z Padre(z, x).
Esta fórmula establece que para cualquier persona x que sea hijo de alguien y, existe al menos una persona z que es padre de x.
3. Hay dos hermanos en la familia, ∃x ∃y (x ≠ y ∧ Hermano(x, y)).
Esta fórmula afirma que existe al menos una persona x y una persona y, distintas entre sí, que son hermanos en la familia.
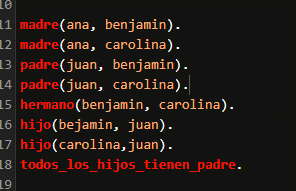
Podrías incluso plantear todo esto en un lenguaje como Prolog.
Empezando por declarar varios hechos como:
· Ana como madre de Benjamin y Carolina.
· Juan como padre de Benjamin y Carolina.
· Benjamin y Carolina como hermanos
Conclusión
Según lo que vimos referente a la lógica de predicados en el ámbito de la Inteligencia Artificial, es evidente que esta herramienta es un componente vital en la capacidad de las máquinas para razonar y tomar decisiones informadas. Ha quedado claro que la lógica de predicados no solo proporciona un marco para representar el conocimiento de manera detallada y sofisticada, sino que también permite a las máquinas interactuar con ese conocimiento de formas dinámicas y significativas.
Hemos ejemplificado cómo la lógica de predicados, con su habilidad para hacer declaraciones sobre "todos" o "algunos" elementos de un conjunto, permite una mayor profundidad y flexibilidad en la representación del conocimiento. Este avance respecto a la lógica proposicional abre un sinfín de posibilidades para la IA, desde el procesamiento del lenguaje natural hasta la toma de decisiones autónomas.
Con el conocimiento adquirido, queda claro que la lógica de predicados es mucho más que un mero concepto teórico: es una herramienta práctica que está remodelando los límites de la Inteligencia Artificial. A medida que continúa su desarrollo y aplicación, no hay duda de que seguirá siendo un componente esencial en la evolución de la IA y en la forma en que las máquinas comprenden e interactúan con el mundo a su alrededor.
Referencias
Russell, S., & Norvig, P. (2016). Artificial Intelligence: A Modern Approach (3rd ed.). Pearson.