A lo largo de la historia se han usado multitud de sistemas numéricos. En realidad, cualquier número mayor que 1 puede ser utilizado como base. Algunas civilizaciones usaban sistemas basados en los números 3, 4 o 5. Los babilonios utilizaron el sistema sexagesimal, basado en el número 60, y los romanos el sistema duodecimal, con el número 12 como base. Los mayas utilizaban el sistema vigesimal, basado en el número 20. El sistema binario, o en base 2, fue usado por algunas tribus antiguas y junto con el sistema en base 16 se usa en la actualidad en los ordenadores o computadoras.
A lo largo de la historia se han usado multitud de sistemas numéricos. En realidad, cualquier número mayor que 1 puede ser utilizado como base. Algunas civilizaciones usaban sistemas basados en los números 3, 4 o 5. Los babilonios utilizaron el sistema sexagesimal, basado en el número 60, y los romanos el sistema duodecimal, con el número 12 como base. Los mayas utilizaban el sistema vigesimal, basado en el número 20. El sistema binario, o en base 2, fue usado por algunas tribus antiguas y junto con el sistema en base 16 se usa en la actualidad en los ordenadores o computadoras.
Representación posicional de los números
Un sistema de numeración en base B, utiliza para representar los números, un alfabeto compuesto por B símbolos o cifras. Así todo número se puede representar por un conjunto de cifras teniendo cada una de ellas un valor dentro del número que depende de:
a) De la cifra en sí.
b) De la posición que ocupa dentro del número.
El sistema de numeración decimal (Base 10) utiliza un alfabeto de diez símbolos {0,1,2,3,4,5,6,7,8,9} y la base tiene valor 10. Por ejemplo, el número 5321.5 puede obtenerse como:
5321.5 = 5000 + 300 + 20 + 1 + 0.5
Osea 3 2 1 0 -1 ß Posiciones de cada cifra dentro del número
5321. 5 = 5 x 103 + 3 x 102 + 2 x 101 + 1 x 100 + 5 x 10-1
Sistema de numeración en base 2 o binario
El sistema de numeración en binario utiliza un alfabeto de dos símbolos {0,1} denominadas cifras binarias o bits y la Base 2.
Ejemplo de número binario sería el 11011010.101
Conversiones de base
Para transformar un número de binario a decimal, se multiplica cada dígito binario por la base elevada al lugar que ocupa el dígito dentro de la cifra:
100111. 11 = 1x25 + 0x24 + 0x23 + 1x22 + 1x21 + 1x20 + 1x2-1 + 1x2-2 = 32 + 4 + 2 + 1 + 0.5 + 0.25 = 39.75
Para transformar un número de decimal a binario
-
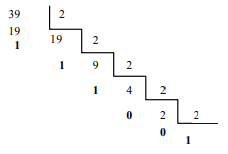
La parte entera binaria se obtiene dividiendo (divisiones enteras) sucesivas veces la parte entera del número decimal y tomando el último cociente y los restos en orden inverso al obtenido:
-
La parte fraccionaria del número binario se obtiene multiplicando por dos la parte fraccionaria del número decimal de partida y las partes fraccionarias que se van obteniendo, tomando como número binario las partes enteras obtenidas:
Se puede utilizar una fórmula para cualquier cambio de base
Ejemplo convertir un número octal a decimal:
25.4(8) ß N(10)
-
Lo primero es identificar la posición
-
Aplicar la fórmula general
N(10) =
-
Efectuar operaciones
N(10) = 2(8) + 5(1) + 4(0.125)N(10) = 16 + 5 + .5 = 21. 5(10)
Ejemplo convertir un número de base cinco a decimal:
142.3(5) ß N(10)
-
Lo primero es identificamos la posición de los dígitos
-
Aplicando la fórmula general
N(10) =
-
Ejecutando la operación
N(10) = 25 + 20 + 2 +.6 = 47.6(10)
Conclusión
El Sistema de Numeración es importante ya que con ellas nosotros cuantificamos las cosas que generamos o que nos rodean, pero nosotros solo estamos acostumbrados a contar en un sistema decimal, desde kinder nos enseñan los numeros decimales, nadie le pone importancia a otro tipo de numeración, pero también es importante conocer otro tipo de sistema de numeración, como lo son los binarios 0-1, el Octal, Hexadecimal. ya que estos son sistemas reconocidos en programacion, un ejemplo claro son los binarios ya que esta numeración esta definida por el cero y el uno, esta numeración es importante aprenderla por que al programar un sistema en una computadora solo reconoce sistemas binarios y no los decimales, esto se debe a los contaste flujos de electricidad que le llega a un computadora o algún otro aparato eléctrico programable.
Referencias