Los arreglos multidimensionales son una herramienta esencial en la programación y gestión de datos, ya que permiten organizar y acceder eficientemente a información estructurada en múltiples dimensiones. Este artículo explora la versatilidad y el poder de los arreglos multidimensionales en la organización y procesamiento de datos, brindando una solución flexible y eficaz para una amplia gama de problemas. Desde la representación de imágenes y matrices numéricas hasta la gestión de bases de datos complejas, estos arreglos ofrecen una estructura sólida para almacenar y manipular información de manera eficiente.
En el campo de la programación y la gestión de datos, es esencial contar con una forma eficiente de organizar la información. Los arreglos multidimensionales, también conocidos como matrices multidimensionales, son una estructura de datos poderosa que permite almacenar y acceder a datos estructurados en múltiples dimensiones. A diferencia de los arreglos unidimensionales (vectores) o los arreglos bidimensionales (matrices), los arreglos multidimensionales ofrecen la capacidad de representar datos en dimensiones adicionales, lo que resulta especialmente útil cuando se manejan grandes cantidades de información.
Segun desarrolloweb.com (2001) “Los arrays multidimensionales son un estructuras de datos que almacenan los valores en más de una dimensión. Dicho de otro modo, un array multidimensional es como un contenedor que guardara más valores para cada posición, es decir, como si los elementos del array fueran a su vez otros arrays” y asi repetidamente aumentando sus dimensiones (Por cada nueva dimension un nuevo indice para moverse en cada una de las posiciones de la dimension).
Ventajas y caracteristicas
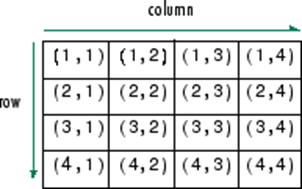
Los arreglos multidimensionales se caracterizan por su capacidad para almacenar elementos en más de una dimensión, lo que los convierte en una estructura de datos versátil y poderosa. Por ejemplo, mientras que los arreglos bidimensionales se pueden visualizar como tablas con filas y columnas, los arreglos tridimensionales pueden interpretarse como una pila de matrices. Esta flexibilidad permite la representación eficiente de datos estructurados, como imágenes en 2D o volúmenes en 3D.
Otra ventaja de los arreglos multidimensionales es su facilidad de acceso a los elementos almacenados. Cada elemento se identifica mediante un conjunto de índices correspondientes a cada dimensión. Por ejemplo, en un arreglo tridimensional, se utilizan tres índices para acceder a un elemento específico. Esto simplifica la manipulación y el procesamiento de datos, ya que se puede acceder directamente a los elementos deseados sin tener que recorrer toda la estructura.
Además, los arreglos multidimensionales ofrecen una amplia gama de operaciones y algoritmos especializados para trabajar con ellos. Por ejemplo, se pueden realizar operaciones de suma, resta y multiplicación de matrices, lo cual resulta invaluable en áreas como la programación lineal y la simulación numérica. También se pueden aplicar algoritmos de búsqueda y clasificación, donde la estructura jerárquica de los datos es esencial para obtener un rendimiento óptimo.
Los arreglos multidimensionales son una herramienta poderosa para organizar y manipular datos estructurados en múltiples dimensiones. Su capacidad de almacenamiento eficiente y acceso directo a elementos específicos los convierte en una elección ideal para resolver problemas complejos en campos como la informática y la investigación científica. Aprovechar su versatilidad y funcionalidad permite a los profesionales abordar desafíos de manera más eficiente y obtener resultados precisos y escalables.
Referencias
Arrays multidimensionales en Javascript. (22 diciembre, 2001). Desarrollo Web. https://desarrolloweb.com/articulos/632.php#:~:text=Los%20arrays%20multidimensionales%20son%20un,utilizamos%20tan%20solo%20un%20%C3%ADndice.
Euroinnova Formación. (2023). Snomed ct. Euroinnova Business School. https://www.euroinnova.cr/blog/latam/arreglo-multidimensional
Imágenes
Arreglos multidimensionales - MATLAB & Simulink - MathWorks América Latina. (n.d.). https://la.mathworks.com/help/matlab/math/multidimensional-arrays.html